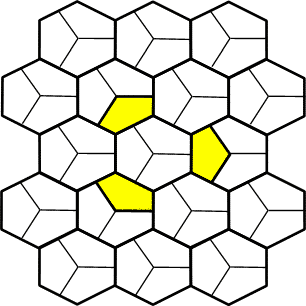
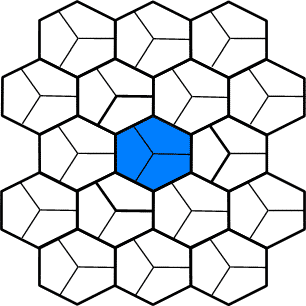
This partitioning scheme is based on a hexagonal map. Each hexagon is divided into three sections. It uses the same update function on each timestep. It does not divide the plane into alternating sub-lattices. It is related to the Star of David partitioning neighbourhood, and to the Tripod neighbourhood. This is probably the most important of the partitioning schemes I have discovered. It has a small number of states per hexagon (3). This number is the smallest that is large enough to support non-linear rules - and thus universal compuatation. Small numbers of states translates into a small look-up table, and a correspondingly compact hardware representation. The main application where such small cells is desirable is performing cellular computation. The idea behind using only a few states is that circuits for most applications have a relatively large ratio of interconnect to logic. The power of large, flexible cells is wasted if they are mainly used in providing interconnection. It's better to have larger numbers of smaller, weaker cells, and to bump up the update frequency. One oddity of the rule is that there's no obvious proof of universality of a uniform, three-bits-per-cell automata, along the same lines as there is for the Q*Bert neighbourhood, or for Morita and Ueno's 8-state triangular scheme. See also the Central Triumphant neighbourhood. |