Invertible Moore automataInvertible Moore automataThe construction yielding a Moore neighbourhood automaton is essentially the same as the one for the Honeycomb neighbourhood.This page essentially only reproduces the diagrams relevant to the Moore neighbourhood. Please refer to the Honeycomb contruction method for additional details. First a path is constructed through the automata, passing through every cell.
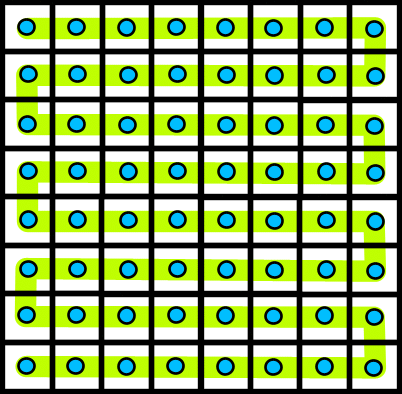 Then, each cell is allocated an update function which is applied on "even" timesteps. This function is such that the state of each cell depends only on it's previous state, and the state of up to three of its neighbours in the previous generation. The three neighbours are chosen in such a way that they are closer to the end of the path in the bottom left-hand corner (with distance being measured along the path). This is illustrated in the following diagram:
 Blue lines from a cell connect it to up to two neighbours. Next, an update function which is applied on "odd" timesteps is allocated to each cell. As before, this function is such that the state of each cell depends only on it's previous state, and the state of up to three of its neighbours in the previous generation. This time, the three neighbours are chosen in such a way that they are closer to the end of the path in the top left-hand corner (again, with distance being measured along the path). The following diagram shows this situation:
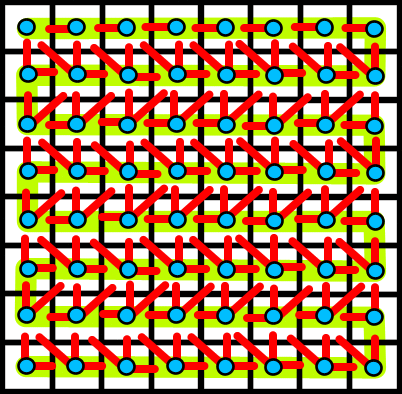 Red lines from a cell connect it to up to three neighbours. Combining the last two diagrams by superposition yields:
 If you now consider the effect of applying both updates simultaneously, you will see that the resulting composite automata uses the Moore neighbourhood. A diagram should help visualise what is happening:
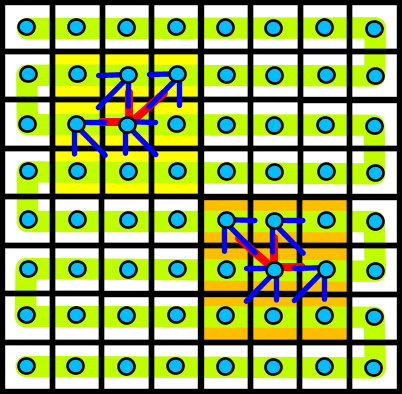 If you apply the "even" (blue) update function first, and then apply the "odd" (red) update function, you will see that the state of the white cells in the diagram above depend on the state of the seven cells in the shaded regions. A single "red" function is involved. This function operates on a domain of four cells - each of which is the result of applying a single "blue" update function to the initial state. Examination of the diagram before this one should indicate that the Moore neighbourhood may be used for every cell in the automata (with suitable truncations applied at the edges).
|