|
We exhibit a reversible three dimensional partitioning cellular automata which
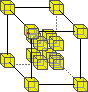
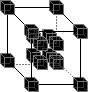
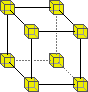
supports universal computation and is time reversal invariant. The model used is derived from Norman Margolus's implementation of a two-dimensional cellular automata based on Edward Fredkin's billiard-ball model which was developed in the process of studying the ultimate physics of computation. Our model is based around the 3D X neighbourhood, which is a simple three-dimensional extension of the X neighbourhood.
The Rule1: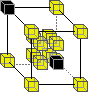 2:
2: 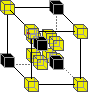 3:
3: 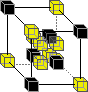 4:
4: 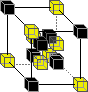 5:
5: 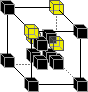
This means that the above rules may be applied in any orientation. All states not explicitly mentioned remain "unchanged" (i.e. the domain is "shrunk" down to form the range).
|