Two-dimensional reversible cellular automata

Fredkin's BBM (Billiard Ball Machine)

Norman Margolus presented a universal, reversible two-dimensional cellular automata based on the "Margolus neighbourhood" partitioning scheme in CAM (Cellular Automata Machines - 1977).

Note that an implementation of the Billiard Ball Machine (in the form of a Java applet) is available as part of our "Diffusion" automata package.

Margolus neighbourhood

Phase one:  ->  Phase two:  =  Temporal alternation:

The automata was based on based on Edward Fredkin's billiard-ball machine, which was developed in the process of studying the "ultimate physics" of computation.

The Rule

Signal propagation

 ->      ->      ->      -> 

Signal interaction

 ->      -> 

Unchanged

 ->      ->      ->      -> 
 ->      ->      ->      -> 

Blank and solid

 ->      -> 

Essentially, billiard-ball automata provide two types of interacting objects, "balls" and "walls". In the automata presented here, both entities are composite objects, a ball being composed of at minimum two active sites, and a wall being made of at least four.

To illustrate how the model simulates the physics of billiard balls and mirrors in an artificial world, here is a 'ball' bouncing on a 'mirror' surface consisting of four wall tiles places in a row, followed by two colliding balls:

         

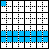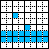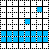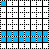
This should help illustrate how signal propagation, signal crossing signal delays and logic gates may be implemented.

Index | HAL | CA | Links
tim@tt1.org | http://alife.co.uk/