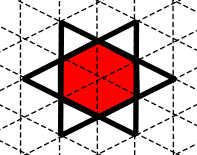
The Star of David neighbourhood is a partitioning scheme often used by those implementing two-dimensional lattice gasses. The automata divides the plane into tesselating hexagons. On each iteration the six triangular sub-cells of domain are used to determine the range via a (usually reversible) map function. The "FHP" Lattice Gas (named after Frisch, Hasslacher and Pomeau) is one of the best known automata that use this neighbourhood. This automata was designed to obey the Navier-Stokes equations in the macroscopic limit. This is something which hexagonal neighbourhoods appear to be able to accomplish with ease, while for rectangular neighbourhoods, appears to be possible only with awkward constructions. Sometimes the domain is modified in such a manner that there are additional cells in the center of each hexagon. These may be used to simulate particles at rest and can assist with simulating other phenomena. A number of models which use lattice gasses have collision rules which are non-deterministic in the case of a head-on collision between two particles. If it is necessary to retain true invertability, another "layer" is sometimes required to act as an invertible random number generator for the process. In the lattice gas literature, this automata is often represented on a triangular lattice, with particles being represented as arrows pointing along the lines from the nodes. Whatever the virtues of this representation, this seems to disguise what constitutes a cell, and hides the hexagonal nature of the automata - an aspect emphasised here. Despite apparent differences, the automata are equivalent. One positive aspect of the Star of David neighbourhood - when compared to the Margolus neighbourhood or the "Q*Bert" neighbourhood is that it performs the same operation on every time step. Many other automata with this property have gained it at the expense of dividing the cellular space into independent alternating sub-lattices - but use of the Star of David neighbourhood avoids this.
|